ANSYS的博客
2020年12月2日
改进有限元模型的3个步骤
发展成功而有效有限元分析(FEA)建模对设计工程师来说是一种令人沮丧的经历。模型需要简单且易于复制,同时还要足够复杂以提供有效的测试结果。这就产生了一个问题,即模型通常过于简化和近似而无法提供准确的分析,或者模型过于复杂而难以处理。不同类型的模型也需要不同类型的网格生成。最后,需要准确地施加载荷以获得准确的结果。我们将讨论这些挑战及其解决方案。
如何改进有限元模型:模型简化
改进有限元模型的一个重要步骤是简化模型。然而,必须以正确的方式简化模型,以实现准确的分析。
以Ansys Sherlock为例进行有限元分析仿真
几何模型的生成是有限元分析中最困难的方面之一。FEA初学者的一个常见错误是假设作为产品设计过程的一部分创建的计算机辅助设计(CAD)模型可以直接插入到FEA研究中。设计师的CAD模型通常包含大量的细节,这些细节需要数小时或数天的处理才能纳入模拟分析。
观看按需网络研讨会“ECAD到FEA 5分钟”以了解更多信息。
然而,这些细节在有限元分析中往往是不必要的。更糟糕的是,在FEA模型中包含不必要的细节会导致网格质量差、模拟运行时间低和结果不准确。
对于分析人员来说,了解何时以及如何简化设计人员传递给他们的模型是进行有效的FEA模拟的关键技能。
有限元分析优化:去除不必要的物体特征
也许可以从大多数CAD模型中立即删除的最常见的细节是圆角和圆角。真正的方边在现实世界中很少存在。边缘通常是圆角的,CAD模型通常会在许多(如果不是全部)几何物体上包含这种圆角。然而,方边要容易得多有限元世界中的网格,大多数小圆角/圆不会影响全局位移计算。CAD工具通常有一个功能来帮助删除圆角/圆角,如填充命令Ansys SpaceClaim.适当地使用这些特性可以快速降低模型的复杂性,而用户只需付出很少的努力。
在Ansys SpaceClaim增量圆去除
结合有效的几何图形和约束
另一种常见的简化方法是删除无关紧要的物体,或者用有效的几何图形或约束替换它们。例如,大多数机械组件包括紧固件,如螺栓和铆钉。有时,可能需要在模型中包含螺栓的几何形状;然而,在许多情况下,螺栓几何形状可以被极大简化的3D几何形状、1D梁单元取代,甚至可以完全删除,并使用刚性接触约束或固定边界条件进行近似。
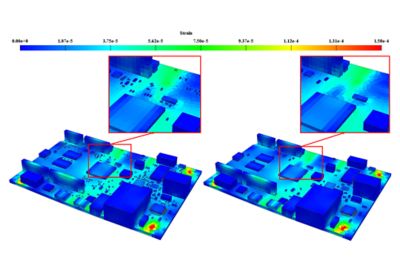
当机械冲击非常小时,其整体和局部影响可以忽略不计
包括芯片组件(左)和不包括芯片组件(右)。
例如,如果在一个12x12英寸的印刷电路板组件(PCBA)上模拟机械冲击,像0201电阻这样非常小的组件将对模型的整体刚度没有影响,可以完全删除。较大的组件,如16 PIN SOIC可能需要建模,但焊料可以替换,并近似为引线和板之间的刚性接触。Ansys夏洛克是一种工具,可帮助从PCBA设计阶段可用的信息中生成fea就绪模型,通过采用用于PCBA制造的ECAD信息,并自动化创建简化的、网格化的、fea就绪的PCBA模型。
如何改进有限元模型:正确的网格生成
除了摧毁一个模型,还需要做出一些正确的决定网格生成.在创建准确的网格时,Ansys-DfR通常考虑三个方面:
- 选择壳元素还是实体元素
- 选择十六进制(砖块)和tet(金字塔)元素
- 选择合适的网孔尺寸和网孔顺序
外壳与实体元素
通常情况下,CAD几何将完全由三维体组成。然而,在有限元模型中,用壳单元而不是实体三维单元来网格这些物体可能更有利。
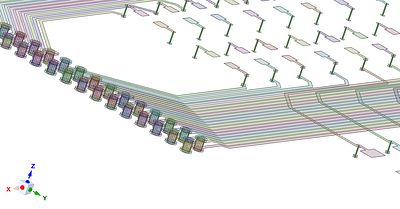
壳元素是3D几何图形的2D近似值,它将物体的厚度存储为物理属性。它们可用于长度远大于车身厚度的薄壁几何图形,并且当剪切变形不显著时(例如,钣金底盘或苏打罐的壁面)。也有特殊的壳和梁加固元件,可以用来模拟薄铜层在一个印刷电路板(PCB).
铜PCB的特点建模为壳和梁加强
Ansys Sherlock中的新功能允许快速生成这些加固几何图形。这些增强使用户能够有效地捕捉痕迹对板变形的影响。
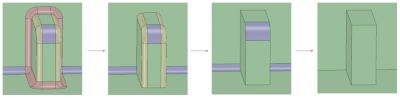
此外,在有限元模型中适当地纳入壳体单元可以大大提高仿真运行时间和结果的准确性。如果使用得当,壳单元通常可以在薄壁结构(如钣金)上生成更高质量的网格,且元素数量要低得多,从而在显著降低计算成本的情况下获得更准确的结果。CAD工具,如Ansys SpaceClaim中的“创建中表面”功能,可以帮助准备壳体网格的几何图形。
使用Ansys SpaceClaim Midsurface Tool将实体(左)替换为表面体(右)。
3D网格划分可以产生更多的细节,从而提供更准确的结果,这似乎是很直观的假设。但情况并非总是如此。特别是在大弯曲的情况下,固体元件在用于网格薄壁几何时经常会产生人为的刚性结构,导致模拟不准确。此外,通过薄壁结构的厚度来细化网格和生成足够的单元以实现精确的位移和应力结果是非常困难的。
此外,如果几何结构足够复杂,当使用固体元素时,薄壁结构可能会导致质量较差的网格,创建具有较差纵横比的银样元素,从而对结果产生负面影响。
十六进制与Tet元素
当决定是否在有限元模型配置中使用六面体(hex)元素或四面体(tet)元素时,重要的是要记住对象本身的整体形状和复杂性。一般的经验法则是尽可能使用六面体元素进行网格划分。与四面体元素相比,十六进制或“砖”元素通常在较少的元素计数下得到更准确的结果。但是,如果对象包含锐角或其他复杂几何图形,则可能需要使用四面体元素进行网格划分。
一个与十六进制元素(左)和tet元素(右)相啮合的相同的身体。
最好是将模型简化到完全用砖块网格化,但这并不总是可行的。对于需要tet网格的复杂几何,请注意确保网格不会导致不准确的结果。这通常意味着更高的元素计数、高阶元素和更长的运行时间。
由于这些原因,任何模型简化,如圆角去除或体分割,允许十六进制网格而不显著改变几何是强烈推荐的。
筛网尺寸和顺序
正确理解网格的顺序和大小是在有限元分析中找到精确结果和合理运行时间之间平衡的关键。
网格尺寸简单地指的是一个元素的特征边缘长度。较小的网格尺寸将导致模型中有更多的元素,从而导致更长的运行时间和更准确的结果。Order描述用于计算元素位移的形状函数。
一阶元素只在元素的角上有节点,并线性计算节点之间的位移。二阶单元包括角间的中间节点,用二次法计算位移。二阶元素中的额外细节通常会提高精度,但会显著增加计算成本。
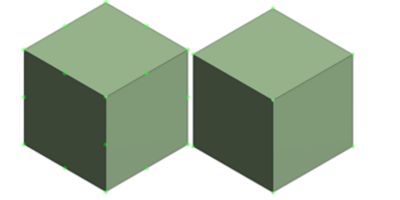
二次元(左)和线性元(右)。节点以绿色突出显示。
注意二阶元素中角之间的中间节点。
生成有效的有限元网格的关键是在所分析的特定问题的顺序和大小之间取得适当的平衡。在可能的情况下,使用二阶元素并迭代细化网格,直到结果收敛。然而,对于更大的问题,即使使用高性能计算也可以在几天内解决,这可能是不可行的。在这些情况下,分析人员将需要使用经验来对网格尺寸和顺序做出适当的决定。
如何改进有限元模型:正确的载荷应用
确定合适的载荷应用是有限元分析的重要步骤。负载应用是测试对象的模型输入,例如热循环、跌落冲击、振动或静态弯曲等特定事件。理解如何应用负载的细微差别对于模拟对象将在现实环境中面对的事件至关重要。
一个常见的示例是确定应用的负载应该应用为静态的还是瞬态的。例如,如果工程师在组装过程中模拟结构的弯曲,将负载建模为静态位移可能是可以接受的,因为应变速率可能要慢得多,并且结果与时间无关。然而,如果工程师正在建模由相同组件掉落引起的类似挠度,他们可能需要使用瞬态模型来捕获相关的惯性效应,因为负载的应用时间要快得多,并且必须捕获与时间相关的效应。
在电子仿真领域,我们在模拟热循环时经常遇到类似的情况。例如,当研究板级(而不是组件级)的热膨胀时,通常可以使用线性材料性质近似值,而静态的、与时间无关的温度斜坡可能是合理的。当分析的重点是板级位移和弹性应力/应变而不是蠕变应变/能量时,这是可以接受的。但是,在研究组件级时焊接疲劳,必须包括随时间变化的焊料蠕变特性。在这种情况下,重要的是准确应用热循环的斜坡和停留时间,而不是简单地线性增加温度。蠕变模型包括随时间变化的特性,因此必须对整个模拟循环进行建模,以最准确地计算用于预测焊料疲劳的蠕变应变/能量结果。
相同的现实世界事件在FEA世界中并不总是相等的,这取决于分析的预期结果。重要的是要始终牢记对象可能面临的现实世界压力,以及这些压力会如何影响兴趣组件。正确地输入这些细微差别将导致准确、有效和可操作的分析。
通过正确的预处理,可以显著提高有限元分析的速度,而不影响其准确性。
观看点播网络研讨会ECAD到FEA只需5分钟了解更多。